A.1 Das Themengebiet der Akustik
Die Akustik ist die Lehre der Entstehung, Ausbreitung und Wahrnehmung von Schall. Hierbei spielen ebenfalls Wellen eine zentrale Rolle. Anstelle von Lichtwellen geht es hier aber natürlich um Schallwellen. Sie weisen einige Ähnlichkeiten zu Lichtwellen auf, aber unterscheiden sich auch in wesentlichen Eigenschaften von ihnen.
Was ist nun Schall? Der Begriff Schall bezeichnet allgemein mechanische Schwingungen in einem elastischen (das bedeutet für eine solche Hin- und Herbewegung geeigneten) Medium. Das Medium kann dabei ein Festkörper, eine Flüssigkeit oder ein Gas sein. Die Teilchen des Mediums bewegen sich und geben diese Bewegung an benachbarte Teilchen weiter. Das kennen wir schon aus der Wärme und Wärmeleitung. Allerdings geht es hier um eine viel geordnetere Bewegung, in der die Teilchen gemeinsam in eine bestimmte Richtung (hin und her) schwingen.
Der Schall breitet sich nämlich in Form einer Verdichtung und Verdünnung des Mediums aus, je nachdem ob die Teilchen gerade „zusammengeschoben“ oder „auseinandergezogen“ werden. Es wird daher von einer „Schallwelle“ gesprochen, die sich im Medium ausbreitet.
Hierbei zeichnet sich schon ein wesentlicher Unterschied zwischen Schall- und Lichtwellen ab: Lichtwellen können sich auch im Vakuum ausbreiten und werden in ihrer Ausbreitung durch Medien sogar derart gestört, dass sie sich langsamer ausbreiten je (optisch) dichter das Medium ist. Dagegen benötigen Schallwellen für ihre Ausbreitung ein Medium. Ohne ein Medium findet keine Schallübertragung statt (siehe Abschnitt C). Dichtere Medien, in denen die Teilchen eng aneinander gekoppelt sind, übertragen sogar besonders schnell den Schall, da die Bewegung sehr leicht auf die nächsten Teilchen übertragen werden kann. So beträgt dich Schallgeschwindigkeit in Luft unter Normalbedingungen ca. 340 m/s. In Wasser breitet sich Schall mit ca. 1480 m/s aus, in Eisen mit 5170 m/s und in Diamant sogar mit 18.000 m/s (siehe auch Abschnitt C.3)!
Was ist nun mit dem Begriff der „Schallwelle“ genauer betrachtet gemeint?
A.2 (Schall-)Wellen
Definition einer Welle: „Eine Welle ist eine regelmäßige (periodische) oder auch einmalige Störung des Gleichgewichtszustands eines Systems, das sich räumlich ausbreitet.“
Was das bedeutet, kann anhand von Wasserwellen betrachtet werden: Die Oberfläche eines Sees befinde sich in Ruhe, also in einem Gleichgewichtszustand, in dem es kleine Bewegung von Teilchen untereinander gibt, die in der Summe weder zu- noch abnehmen und keine Vorzugsrichtung haben. Wird nun einen Stein ins Wasser geworfen, verursacht der Aufprall des Steins auf der Wasseroberfläche eine Störung. Das Wasser wird am Auftreffort nach unten gedrückt, schwingt wieder zurück und über die Höhe des Wasseroberfläche hinaus, wieder nach unten usw. Diese Schwingung breitet sich kreisförmig in alle Richtungen aus, weil die Wasserteilchen die Bewegung an ihre Nachbarteilchen weitergeben. Es entstehen auf der Wasseroberfläche konzentrische Kreise, die radial nach außen laufen (siehe Abbildung A1).

A.3 Graphische Darstellung einer Schallwelle
Im Themengebiet Licht & Schatten sind graphische Darstellungen von Lichtwellen abgebildet. Bei einer Schallwelle ist diese Darstellungsform nun noch etwas leichter nachzuvollziehen. Wellen werden üblicherweise auf zwei verschiedene Arten dargestellt, die beinahe identisch aussehen. Im einen Fall wird allerdings die x-Achse als räumliche und im zweiten Fall als zeitliche Achse betrachtet.
1. Die Bewegung der Welle im Raum:
Wird ein Querschnitt durch die Kugelwelle gelegt und die Ausbreitung von ihrem Zentrum aus betrachtet, dann ist die Wasseroberfläche jeweils abwechselnd nach oben und unten von der Ruhelage aus betrachtet ausgelenkt (siehe Abbildung A2). Wird die x-Achse als Raumrichtung vom Zentrum nach außen definiert, dann stellt die zur Welle geformte Oberfläche des Wassers eine Sinuskurve dar. Auf der y-Achse ist dabei die Höhe der Auslenkung A aufgetragen.

Eine solche Darstellung einer Welle ist sinnvoll, wenn ihre Ausbreitung im Raum betrachtet wird – beispielsweise, wie sich der Schall von der Gitarre zum Ohr ausbreitet (siehe Abschnitt C),
Die Bewegung der Welle im Laufe der Zeit:
Betrachtet wird nun die Welle an nur einem Ort auf der Wasseroberfläche. Stellen wir uns vor, dort einen kleinen Schwimmer zu positionieren, der immer mit der Wasseroberfläche auf- und abschwingt. Seine zeitliche Bewegung kann ebenfalls graphisch dargestellt werden, wobei die x-Achse nun nicht den räumlichen, sondern den zeitlichen Verlauf widerspiegelt (siehe Abbildung A3).

Ein solcher zeitlicher Verlauf ist sinnvoll, wenn die Art des Schalls betrachtet soll, wie er an einem bestimmten Ort zu hören ist. Dann wird der Schall an diesem Ort mit einem Mikrophon aufgenommen (s.u.). Der zeitliche Verlauf der Schwingung lässt sich aber auch mit einem kleinen Trick sichtbar machen. Betrachten wir eine Stimmgabel, die angeschlagen wird. Dadurch beginnt sie zu schwingen und gibt einen für sie charakteristischen Ton von sich. Die Schwingung einer Stimmgabel ist aber in der Regel zu schnell, als dass wir sie mit den Augen wahrnehmen und erkennen könnten, wie sie genau vonstatten geht. Wird allerdings ein kleiner Stift oder eine Spitze an ein Ende der Stimmgabel montiert und zieht man sie während des Schwingens schnell über ein Papier oder eine gerußte Platte, dann wird diese Schwingung sozusagen entlang der x-Achse (in Zieh-Richtung) zeitlich auseinandergezogen. Das folgende Video A1 zeigt dies anhand einer 128Hz Stimmgabel. Dabei zeigt sich hier deutlich der sinusförmige Verlauf der Schwingung.
Video A1: Auseinanderziehen einer angeschlagenen Stimmgabel über eine Rußplatte.
Die wichtigen Größen zur Beschreibung einer Welle:
Eine Welle wird beschrieben durch die Größen Periode, Periodendauer, Wellenlänge, Frequenz und Amplitude. Charakteristisch für das jeweilige Medium kommt noch die Ausbreitungsgeschwindigkeit hinzu. Abbildung A4 fasst die Bedeutung der fünf Begriffe noch einmal an der graphischen Darstellung zusammen.

Eine Periode bezeichnet einen kompletten Durchgang der Schwingung, beispielsweise vom Punkt der größten Auslenkung durch die Ruhelage in den Punkt der niedrigsten Auslenkung durch die Ruhelage und zum Punkt der größten Auslenkung zurück.
Die Periodendauer T beschreibt die Zeit, die eine solche komplette Schwingung benötigt. Bei der oben dargestellten Schwingung wären dies gerade T=0.02s.
Die Frequenz f ist der Kehrwert dieser Periodendauer, sie beschreibt, wie viele Schwingungen pro Sekunde durchlaufen werden können. Im oberen Fall wären das f=1/T=50Hz. Da auf Schallwellen je nach ihrer Frequenz unterschiedliche Rezeptoren im Ohr ansprechen, können Schallwellen anhand ihrer Frequenz von uns unterschieden werden. Je höher die Frequenz, desto höher wird der Schall wahrgenommen (siehe Abschnitt D).
Die Amplitude A misst den Wert der maximalen Auslenkung. Sie gibt sozusagen die „Stärke“ der Welle an. Im Fall der Schallwelle wäre das die Lautstärke des Schalls. Je stärker die Schwingung der Teilchen, desto stärker werden auch die Schallrezeptoren im Ohr angeregt, wenn die Schallwelle dort eintrifft (siehe Abschnitte C und D). Der Schall wird als lauter wahrgenommen.
Die Ausbreitungsgeschwindigkeit c ergibt sich ebenso wie bei der Ausbreitung einer Lichtwelle nach der Gleichung![]() In den bisher betrachteten Beispielen hatten wir es mit sehr regelmäßigen, sinusförmigen Schwingungen zu tun, wie sie beispielsweise bei einer Stimmgabel vorkommen, die einen „reinen Ton“ erzeugt. Schallwellen können aber sehr unterschiedlich aussehen und sich aus vielen einzelnen Beiträgen zusammensetzen. Üblicherweise werden daher vier Arten von Schall unterschieden. Für die Unterscheidung dieser Schallarten sind graphische Darstellungen sehr nützlich. Dafür wird die x-Achse wie in Abb. A.3 als Zeitachse verwendet. Ein Mikrophon nimmt an einem bestimmten Ort die Schallwelle auf und wandelt sie in ein elektrisches Signal um, das von einem Oszilloskop in die graphische Darstellung umgesetzt wird. Oszilloskope befinden sich beispielsweise in Physiksammlungen – oder auch mit Hilfe einer App auf dem Handy (beispielsweise mit der App Phyphox – Funktion Akustik / Oszilloskop).
In den bisher betrachteten Beispielen hatten wir es mit sehr regelmäßigen, sinusförmigen Schwingungen zu tun, wie sie beispielsweise bei einer Stimmgabel vorkommen, die einen „reinen Ton“ erzeugt. Schallwellen können aber sehr unterschiedlich aussehen und sich aus vielen einzelnen Beiträgen zusammensetzen. Üblicherweise werden daher vier Arten von Schall unterschieden. Für die Unterscheidung dieser Schallarten sind graphische Darstellungen sehr nützlich. Dafür wird die x-Achse wie in Abb. A.3 als Zeitachse verwendet. Ein Mikrophon nimmt an einem bestimmten Ort die Schallwelle auf und wandelt sie in ein elektrisches Signal um, das von einem Oszilloskop in die graphische Darstellung umgesetzt wird. Oszilloskope befinden sich beispielsweise in Physiksammlungen – oder auch mit Hilfe einer App auf dem Handy (beispielsweise mit der App Phyphox – Funktion Akustik / Oszilloskop).
A.4 Schallarten
Hören Sie sich die 4 verschiedenen Schallarten im folgenden Video A2 an.
Jedes der Hörbeispiele repräsentiert jeweils eine der vier Kategorien:
-
-
-
- den Ton
- den Klang
- das Geräusch
- den Knall
-
-
Worin unterscheiden sich diese vier Schallarten und wie entstehen sie? Hierfür wird die zeitliche Darstellung auf dem Oszilloskop betrachtet.
Video A2: Betrachtung eines Tons im Oszilloskop.
Video A3: Betrachtung eines Klangs im Oszilloskop.
Video A4: Betrachtung eines Geräuschs im Oszilloskop.
Video A5: Betrachtung eines Knalls im Oszilloskop.
Für die vier in den oberen Videos hörbaren Schallbeispiele ergeben sich die folgenden Darstellungen (Abbildung A5):

Im Folgendem werden die verschiedenen Schallkategorien nacheinander betrachtet.
Der Ton
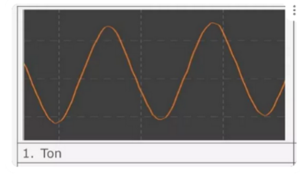
Bei einem „Ton“ wird als Oszilloskopbild eine Sinusschwingung (siehe Abbildung A6) erhalten. Ein Ton ist in der Physik dadurch definiert, dass er eine Schwingung mit nur einer einzelnen Frequenz darstellt. Das ist im Alltag nur sehr selten der Fall – beispielsweise bei einer guten Stimmgabel oder dem Testton / Besetztton in Telefon / Fernseher. In beiden Fällen handelt es sich um den sogenannten „Kammerton a“ von 440 Hz, der in Abbildung A6 dargestellt ist. Im Alltag wird der Begriff „Ton“ in einem viel weiter gefassten Zusammenhang (beispielsweise ein Ton gespielt auf dem Klavier oder der Flöte, ein gesungener Ton) verwendet. Bei fast allen dieser Fälle handelt es sich aus Sicht der Physik allerdings um einen Klang.
Der Klang

Bei einem Klang ergibt sich ein Oszilloskopbild, das zwar periodisch, aber nicht rein sinusförmig aussieht. Das liegt daran, dass ein Klang nicht nur einen Ton, bzw. Schall einer Frequenz enthält, sondern mehrere. Diese einzelnen Sinusschwingungen überlagern (addieren) sich zu einer Gesamtschwingung (mehr dazu in Abschnitt E zu Obertönen). Da diese einzelnen Sinusschwingungen alle periodisch sind, ergibt sich auch wieder eine periodische Gesamtschwingung (siehe Abbildung A7). Diese ist allerdings auf Grund der mehreren addierten Beiträge im Gegensatz zum Ton nicht mehr sinusförmig. Wenn im Alltag / in der Musiksprache von einem „Klang“ gesprochen wird, ist dabei beispielsweise das Erklingen mehrerer Gitarrensaiten gleichzeitig gemeint. Aus Sicht der Physik handelt es sich wie in Abbildung A7 zu sehen aber bereits bei dem Erklingen nur einer Gitarrensaite bereits um einen Klang. Denn in diesem Schall sind neben dem angespielten Grundton noch andere Töne zu hören, die „Obertöne“ genannt werden. Diese machen erst den „vollen Klang“ eines Instrumentes aus, denn eine Gitarrensaite klingt ganz anders als eine Stimmgabel, auch wenn sie beide den gleichen Grundton anspielen. Zum einfachen Vergleich mit dem Oszilloskopbild der Stimmgabel in Abbildung A6 handelt es sich bei Abbildung A7 um den Klang der a-Saite einer Gitarre. Der dominierende Grundton a gibt den grundsätzlichen Verlauf der Schwingung vor, d.h. die Schwingung hat eine Periodendauer von T = 1/440Hz = ca. 0,002s. Die Sinusform des reinen Tons ist aber durch periodische „Einbuchtungen“ von weiteren Frequenzen verändert. Diese Frequenzen sind nicht irgendwelche beliebigen, sondern alle Vielfache der Grundschwingung. Das ist sehr wichtig, denn so bleibt die grundsätzliche Periodizität des Grundtons bestehen. Abbildung A8 verdeutlicht dies am einfachen Beispiel des Grundtons mit Frequenz f (in rot) und dem ersten Oberton mit (doppelter) Frequenz (2f, in blau). Die beiden addieren sich zum Klang (in grün), der mit derselben Periodizität schwingt wie der Grundton.

Dass ein Instrument nicht einzelne Töne, sondern Klänge spielt, ist auch durch eine logische Überlegung ersichtlich: Der Ton „a“ ist immer gleich, denn er besteht nur aus der einen Frequenz. Wenn Instrumente Töne spielen würden, könnten wir sie also überhaupt nicht voneinander unterscheiden: Ein Stimmgabel-a würde sich identisch anhören wie das a einer Gitarre, eines Klaviers, einer Geige… Der spezifische Klang der Instrumente kommt erst durch die spezifischen Anteile der Obertöne zustande. (Mehr dazu in Abschnitt E.)
Abbildung A9 und A10 zeigen dies noch einmal im direkten Vergleich zwischen dem Schall einer Stimmgabel und eines Klaviers:


Interessant ist es auch, sich unsere Sprache hier genauer anzuschauen: Vor allem Vokale sind ebenfalls in die Kategorie Klang einzuordnen (siehe Abschnitt E1 zur menschlichen Stimme).
Das Geräusch

Bei einem Geräusch ist ein nicht-periodisches Oszilloskopbild zu erkennen (siehe Abbildung A11). Hier schwingen wie beim Klang ebenfalls viele verschiedene Frequenzen mit und addieren sich zum Gesamtschall – und zur Gesamtkurve auf dem Oszilloskop. Allerdings handelt es sich hierbei um einen weniger geordneten Mix als beim Klang: Die einzelnen Beiträge haben keine gemeinsame Grundfrequenz, sondern können alle möglichen Frequenzen besitzen. Darüber hinaus kommen Frequenzen hinzu, brechen wieder ab usw. Da also derart nicht-geordnete Zustände vorliegen, kommt es auch zu keiner Regelmäßigkeit (Periodizität) des Schalls. Es ist ein Geräusch zu hören. Beispiele hierfür sind alle möglichen Varianten von Rauschen, Papierzerknüllen, Zischen usw.
Der Knall

Ein Knall enthält wie ein Geräusch ein ungeordnetes Gemisch verschiedener Frequenzen. Im Unterschied zum Geräusch ist es allerdings grundsätzlich kurz (und meist laut). Auf dem Oszilloskop zeigt sich darum ein kurzer Ausschlag mit hoher Amplitude (siehe Abbildung A12).
Ähnlich wie bei den vier Arten von Wechselwirkungen von Licht an Oberflächen sind auch diese vier Kategorien natürlich als Idealformen zu verstehen, zwischen denen es weniger eindeutige Zwischenformen geben kann. So gehen beispielsweise ein länger andauernder Knall ebenso wie ein unreiner Klang in ein lautes Geräusch über und umgekehrt. Die Unterscheidung kann aber zur grundsätzlichen Einordnung von Schall dienen und ist für die meisten Schallphänomene auch gut zu bestimmen.
Alles verstanden? Auf dieser Website sind ein paar Fragen zu den behandelten Inhalten zu finden. Sie sollen dem Verständnis und einer nachhaltigen Erkenntnisgewinnung dienen.
